Published 12 October 2019

This blog post serves as an accompanying article to the introduction to functional programming talk given as part of Solirius’ internal training. The slides are also available online.

What makes programming functional?

Functional programming is often thought of as an alternative to object oriented programming, but this is not strictly true. Functional programming is an alternative to imperative programming that aims to be declarative and grounded in mathematics.

An imperative program will modify the program’s state in the computers memory to achieve the desired outcome. Whereas a functional program will apply a series of functions that transform data to the correct output. For example, an imperative function that returns the number of integers in an array that are greater than 10 might look like this:

function countGreaterThan10(numbers) {
  let total = 0;

  for (const num of numbers) {
    if (num > 10) {
      total++;
    }
  }

  return total;
}

Whereas a more functional approach would be:

function countGreaterThan10(numbers) {
  return numbers.filter(n => n > 10).length;
}

This approach creates a new array of integers with a value greater than 10 and then returns the length of that array. Not only is this approach a lot less lines of code but it’s more declarative and arguably easier to read.

Higher order functions

One of the tenets of functional programming is that a function is just a type of data, and like any other data it can be passed to another function as an argument. When a function is passed to another function it’s referred to as a higher order function.

The functional example of countGreaterThan10 makes use of a higher order function to filter the array before returning it’s length.

Another common example of higher order functions is the map function. In order to get the square root of every number in an array an imperative program would iterate over the array and calculate the values:

function sqrtAll(values) {  
  for (const i in values) {
    values[i] = Math.sqrt(value);
  }

  return values;
}

It’s possible to achieve the same result using the map function. This function applies a higher order function to every item an array and returns a new array with the result of each operation.

function sqrtAll(values) {
  return values.map(x => Math.sqrt(x));
}

As with the previous example this is both more concise and more declarative. One of the other benefits of this approach is that it is a pure function - it returns a new array rather than modifying one that is given to it.

Purity

State and mutability are things that are often mentioned in the same breath as functional programming. That’s because another of the key tenets of functional programming is that functions should be “pure”.

A pure function has no side effects, that is to say that they do not depend on or mutate any state outside of the function.

Pure functions are incredibly easy to test, they take 0 or more inputs and return a value. This means no mocking of dependencies or setting test harness to get the system in the correct state. Just simple input / output.

Mutability

Some functional programming languages do not allow any mutability at all, but that does not necessarily mean that all immutability is bad. Just that it should be contained and encapsulated so that it doesn’t affect other areas of the program.

Category theory and composition

One of the nice features of pure functions is that you can start reason about them using mathematics, specifically a branch of mathematics called category theory. For example, given we have a function f that transforms a value X -> Y and a function g that transforms a value Y -> Z then you can compose functions f and g to transform X -> Z.

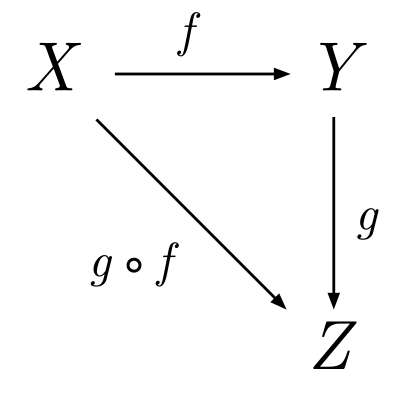
This is idea is known as functional composition. One way of composing functions is to chain them together:

const result = countGreaterThan10(sqrtAll(filterEven([1, 5, 10, 15, 20, 25])));

But this approach quickly becomes unwieldy. Using the knowledge we have about category theory it is possible to make a function that will automatically combine many functions together into a single new function.

function compose(...fns) {
  return function (arg) {
    return fns.reduceRight((lastResult, fn) => fn(lastResult), arg);
  }
}

const numEvenAndSqrtGreaterThan10 = compose(
  filterEven, 
  sqrtAll,
  countGreaterThan10
);

const result = numEvenAndSqrtGreaterThan10([1, 5, 10, 15, 20, 25]);

The implementation of compose introduces another common functional idea: reduce. The reduce function abstracts away much of the boilerplate code often associated with iteration by simplifying it to a higher order function the takes the result so far, the current item in the array and then returns the result of applying the current item to the result so far.

Functional composition is such a common pattern that JavaScript is adopting a pipeline operator to better support it:

const result = [1, 5, 10, 15, 20, 25] |> filterEven |> sqrtAll |> countGreaterThan10; 

Partial application (or currying)

So far the examples have used quite a simple composition, the result of each method is passed to the next. Real world situations can become much more complex and we often need to apply multiple arguments to functions and then compose them. In these situations it may be necessary to partially apply some arguments to a function before it is called.

function curry(fn, arguments) {
  return function (remainingArguments) {
    return fn(...arguments, ...remainingArguments)
  }
}

function addToAll(amount, numbers) {
  return numbers.map(n => n + amount);
}

const add100ToAll = curry(addToAll, 100);

const result = [1, 5, 10, 15, 20, 25] 
  |> add100ToAll 
  |> filterEven 
  |> sqrtAll 
  |> countGreaterThan10; 

Where next

Through practical examples we’ve looked at Higher Order Functions, Pure Functions, Composition, Currying and a little bit of Category Theory. Quite a tall order for an introduction, you won’t be surprised to hear there is a lot more to explore behind each of these areas. Feel free to dig into each area in more detail but it’s not necessary to get started with functional programming. Putting these ideas into practice will often highlight the path forward.

I also have a post available about refactoring from common imperative patterns to more functional ones.