Published 14 November 2019

The concept behind Hannah Bast’s transfer patterns is brilliantly simple: pre-calculate all the points a passenger may need to change for every possible journey in the network and perform real-time queries by linking together these points for specific times.

The original paper suggests using Dijkstra Algorithm to reconstitute journeys from transfer patterns but does not go in to much detail, this post explores a couple of implementations of a journey planner based on transfer patterns.

A simple approach

There are a number of ways to store transfer patterns, but for the initial approach it’s best to use a simple list of stops where the passenger changes to another service. For example, the journey A→E might contain the following patterns:

A,B,C,E
A,B,D,E
A,C,E
A,C,D,E

In order to turn these transfer patterns into journeys, process them individually and turn them into a list of origin and destination pairs representing one leg of the journey. For the transfer pattern A,B,C,E this would be:

[A,B],[B,C],[C,E]

Then look up all the trips operating between each pair of stops in the pattern. The relevant part of these trips can be cut into a journey leg that runs between the origin and destination:

A→B
d10:00,a10:30
d11:00,a11:30
d12:00,a12:30

Creating an index of trips

Scanning all the trips in a dataset to extract legs is expensive so it’s best build up an index of trips that pick up and drop off at particular stations when the data set is loaded.

This example code iterates every stop of every journey to create the index:

const legIndex = {};

for (const trip of trips) {
  for (let i = 0; i < trip.stopTimes.length - 1; i++) {
    if (trip.stopTimes[i].pickUp) {
      const origin = trip.stopTimes[i].stop;

      for (let j = i + 1; j < trip.stopTimes.length; j++) {
        if (trip.stopTimes[j].dropOff) {
          const destination = trip.stopTimes[j].stop;

          legIndex[origin] = legIndex[origin] || {};
          legIndex[origin][destination] = legIndex[origin][destination] || [];
          legIndex[origin][destination].push(trip.toLeg(origin, destination));
        }
      }
    }
  }
}

Completing the journey

Given a list of legs between every pair of stops, it’s possible to progressively scan through those pairs to find a leg that departs the origin station on or after the target departure time.

After each transfer to the next leg the target departure time is updated to reflect the arrival time of the previous leg.

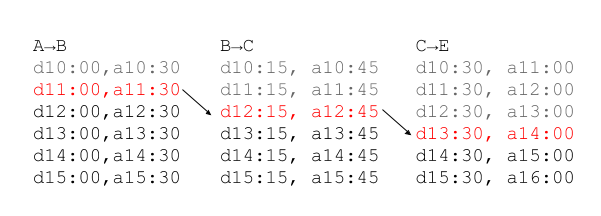
If it is possible to progress to the final leg and find a trip then a complete journey can be made, otherwise the journey is not possible.

const patternStops = [[A,B],[B,C],[C,E]];

function getJourney(legIndex, patternStops, departureTime) {
  const legs = [];

  for (const [origin, destination] of patternStops) {
    const leg = legIndex[origin][destination].find(t => l.departureTime >= departureTime);

    if (!leg) {
      return null; // journey not possible
    }

    legs.push(leg);
  }

  return legs;
}

Cleaning up results

Doing this for a large number of transfer patterns will result in a long list of journeys, many of which will be redundant as they are slower than other journeys. These can be removed by using a filter that removes slower journeys unless they have fewer legs.

Range queries

One of the benefits of this approach is that it is well suited to range queries, where a number of results are required. By extracting all the trips available between the first leg it’s possible to construct a journey for each departure.

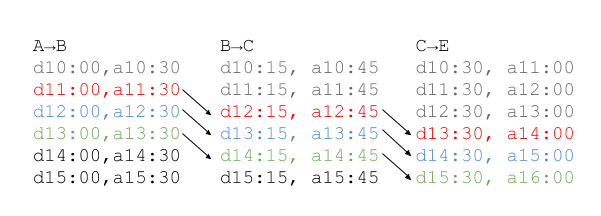
As each subsequent journey will only ever arrive at the same time or later, it’s possible to optimize the scanning by maintaining an index of the last leg found for each origin / destination and searching from that point on. This index only applies within the context of a single transfer pattern, other transfer patterns need to maintain their own index.

Tree compaction

It’s quite common for transfer patterns to contain a lot of duplication. Looking at the original transfer patterns:

A,B,C,E
A,B,D,E
A,C,E
A,C,D,E

The first leg of transfer patterns 1 and 2, and 3 and 4 are the same. By converting the transfer patterns into a directed acyclic graph (a tree) it’s possible to eliminate some of that duplication.

     A
   /   \
  B     C
/   \   | \
C   D   E  D
|   |      |
E   E      E   

The overall process is the same but at each node with multiple children the journey so far is cloned and continued down each path independently.

function getJourneys(patternNode, legs, departureTime) {
  const leg = patternNode.findLeg(departureTime);

  // journey can't be completed
  if (!leg) {
    return [];
  }

  // reached the end of the pattern
  if (patternNode.children.length === 0) {
    return [[...legs, leg]];
  }

  return patternNode.flatMap(n => getJourneys(n, [...legs, leg], leg.arrivalTime));
}

Dijkstra

There is still some duplication in the graph, between C->E and D->E. The natural continuation of the previous approach is to compact all patterns into a single graph and run a modified version of Dijkstra’s shortest path algorithm. In doing this it is no longer possible to track the last returned journey along each edge of the graph as there is no guarantee that edges are scanned in time order. In my testing this meant that Dijkstra’s algorithm was consistently slower than the previous approach.

Another disadvantage of this approach is it becomes harder to return results from multiple transfer patterns. It will always return the journey with the earliest arrival time, regardless of whether it has more changes.

Conclusion

Transfer patterns are still the fastest way to perform real-time queries, even if they do require a large amount of preprocessing. We’ve seen two novel approaches to journey planning that perform well. The first approach is simpler to implement but does not perform as well on routes with many transfer patterns of a similar nature. The second approach is more complex but performs very well in situations where there is a lot of duplication between transfer patterns. This is especially relevant for queries where the destination is a list of stations rather than a single station.

The original paper recommends using Dijkstra’s algorithm and it is possible that certain implementations of it perform better than these approaches but the simple optimizations make these approaches after than a stock Dijkstra’s algorithm.

Open source implementations of the tree compacted approach is available GitHub:

https://github.com/planarnetwork/transfer-pattern-planner